Operasi Aritmatika merupakan penjumlahan dan juga pengurangan, sementara perkalian dan pembagian merupakan operasi selanjutnya yang dikembangkan dari kedua operasi dasar tersebut.
Berikut akan kami berikan materi mengenai operasi Aritmatika Bilangan Biner, Oktal, serta Heksadesimal.
1. Operasi Aritmatika Bilangan Biner
Aritmatika Bilangan Binner merupakan beberapa operasi perhitungan yang terjadi dalam bilangan biner.
Terdapat 5 operasi aritmatika pada bilangan biner, antara lain:
- Penjumlahan
- Pengurangan
- Perkalian
- Pembagian
- Bilangan Biner Bertanda
A. Penjumlahan Bilangan Biner
Dalam bilangan biner terdapat dua aturan dasar, antara lain:
0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 1, simpan 1
1 + 0 = 1
0 + 1 = 1
1 + 1 = 1, simpan 1
Sebagai cara penjumlahan bilangan desimal yang kalian kenal sehari-hari, penjumlahan bilangan biner juga harus selalu memperhatikan carry (sisa) dari hasil penjumlahan pada tempat yang lebih rendah.
Sebagai contoh:
Soal 1.
1111 2
10100 2
_______+
100011 2 Carry of 1 (3 kali)
10100 2
_______+
100011 2 Carry of 1 (3 kali)
Soal 2.

Dalam contoh diatas, telah dilakukan penjumlahan 8 bit tanpa carry, sehingga hasil penjumlahnya masih berupa 8 bit data. Untuk contoh berikutnya akan dilakukan penjumlahan 8 bityang menghasilkan carry.
Soal 3.
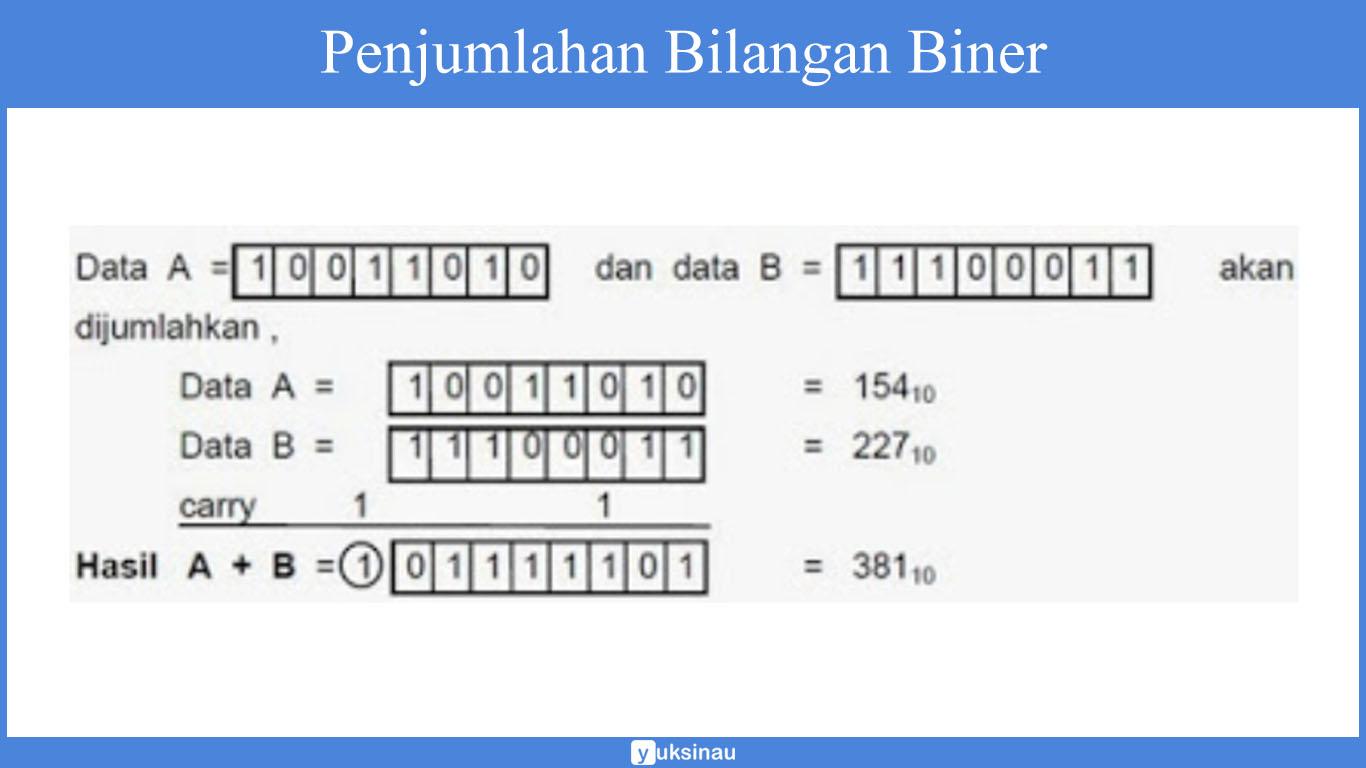
Hasil penjumlahan diatas menjadi 9 bit data, sehingga untuk 8 bit data, hasil penjumlahannya bukan merupakan jumlah 8 bit data A dan B tetapi bit yang e-8 (dihitung mulai dari 0) atau yang disebut carry juga harus diperhatikan sebagai hasil penjumlahan.
B. Pengurangan Bilangan Biner
Pada bilangan biner terdapat dua cara dalam pengurangan yakni dengan 1s complement dan 2s complement, Perbedaan diantara keduanya antara lain:
- 1s complement
merupakan sebuah cara untuk membalikkan bilangan negatif menjadi positif (sebab sebenarnya dalam bahasa komputer tidak kenal operasi pengurangan).
Sehingga operasi pengurangan ini akan menjadi penjumlahan.
1s complement dari sebuah bilangan dilakukan dengan mengubah 0 menjadi 1 dan 1 menjadi 0. Sebagai contoh:
- 2s complement kurang lebih mempunyai fungsi yang sama dengan 1s complement yakin membuat sebuah bilangan negatif menjadi positif. Tetapi cara 2s complement sedikit ada perbedaan yakni 1s complement yang ditambah dengan 1. Sebagai contoh:
 Lalu
Lalu 
Sehingga 2s complement dari 10001 yaitu 01111 dan 1s complement-nya yaitu 01110.
C. Perkalian Bilangan Biner
Dilakukan sama dengan cara perkalian yang terdapat dalam operasi bilangan desimal. Dasar perkalian pada bilangan biner ialah sebagai berikut:
0 x 0 = 0
1 x 0 = 0
0 x 1 = 0
1 x 1 = 1
1 x 0 = 0
0 x 1 = 0
1 x 1 = 1
Sebagai contoh:
Soal 1.
1110 2
1100 2 x
0000
0000
1110
1110 +
10101000 2

D. Pembagian Bilangan Biner
Pembagian biner dilaksanakan dengan menggunakan cara yang sama dengan yang ada pada bilangan desimal. Pembagian biner 0 tidak memiliki arti, sehingga dasar pembagian pada bilangan biner adalah sebagai berikut:
0 : 1 = 0
1 : 1 = 1
1 : 1 = 1
Contoh #1:
101 / 1111101 \ 11001
101 _
101
101 _
0101
101 _
0

2.Operasi Aritmatika Bilangan Oktal
A. Penjumlahan Bilangan Oktal
Berikut adalah tahapan untuk operasi penjumlahan oktal, antara lain:
- tambahkan masing-masing kolom secara desimal
- rubah dari hasil desimal ke dalam bilangan oktal
- tuliskan hasil dari digit paling kanan dari hasil oktal
- jika hasil penjumlahan pada masing-masing kolom terdiri dari dua digit, maka digit paling kiri adalah carry of untuk penjumlahan kolom berikutnya.
- sisa akan muncul atau terjadi apabila jumlahnya sudah melebihi 7 pada setiap tempat.
Sebagai contoh:

B. Pengurangan Bilangan Oktal
Pengurangan Oktal bisa dilakukan dengan cara yang sama dengan yang ada pada operasi pengurangan bilangan desimal.
Pada pengurangan apabila bilangan yang dikurangi lebih kecil dari pada bilangan pengurangnya maka akan dilakukan peminjaman (borrow) pada tempat yang lebih tinggi (dengan nilai 8).
Sebagai contoh:
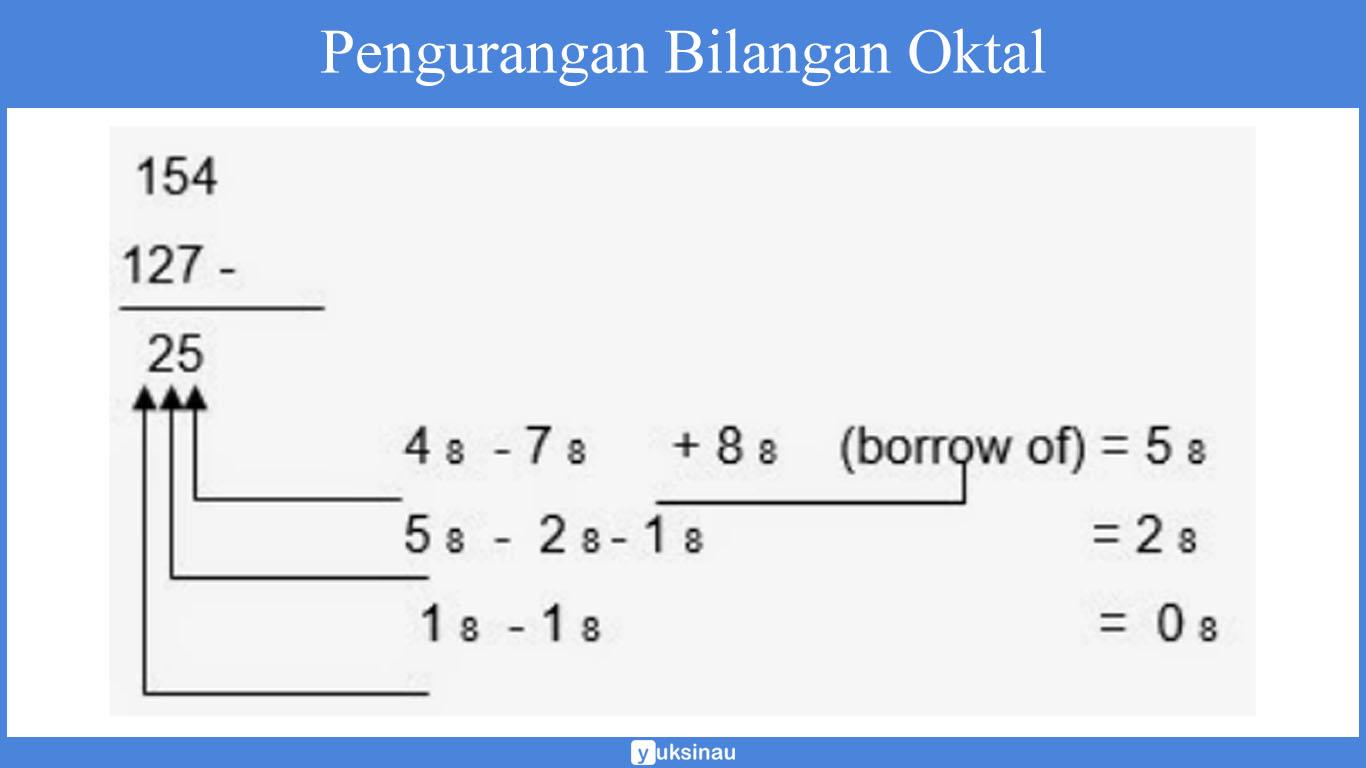
C. Perkalian Bilangan Oktal
Berikut adalah tahapan untuk operasi perkalian oktal, antara lain:
- kalikan masing-masing kolom secara desimal.
- rubah dari hasil desimal ke bilagan oktal.
- tuliskan hasil dari digit paling kanan dari hasil oktal.
- jika hasil perkalian pada masing-masing kolom terdiri atas 2 digit, maka digit paling kiri adalah carry of untuk ditambahkan pada hasil perkalian pada kolom berikutnya.

D. Pembagian Bilang Oktal
 3. Operasi Aritmatika Bilangan Heksadesimal
3. Operasi Aritmatika Bilangan Heksadesimal
A. Penjumlahan Bilangan Heksadesimal
Dalam penjumlahan bilangan heksadesimal, sisa akan terjadi atau berlangsung apabila jumlah dari masing-masing tempat melebihi 15.
Sebagai contoh:


B. Pengurangan Bilangan Heksadesimal
Pada pengurangan apabila bilangan yang dikurangi lebih kecil dibandingkan dengan bilangan pengurangnya maka akandilakukan peminjaman (borrow) pada tempat yang lebih tinggi (dengan nilai 16).
Sebagai contoh:

C. Perkalian Bilangan Heksadesimal
Berikut adalah tahapan untuk operasi perkalian heksadesimal, antara lain:
- kalikan masing-masing kolom secara
- rubah dari hasil desimal ke oktal
- tuliskan hasil dari digit paling kanan dari hasil bilangan oktal
- jika hasil perkalian pada masing-masing kolom terdiri atas 2 digit, maka digit paling kiri adalah carry of untuk ditambahkan pada hasil perkalian kolom berikutnya.
Sebagai contoh:

D. Pembagian Bilangan Heksadesimal
Pembagian pada bilangan Heksadesimal sama halnya seperti yang ada dalam pembagian pada bilangan decimal.
Sebagai contoh:

Increment dan Decrement
Increment (bertambah) dan Decrement (berkurang) merupakan dua pengertian yang sering sekali dipakai dalam teknik miroprosessor.
Dalam matematik pengertian increment yaitu Bertambah Satu dan decrement berarti Berkurang Satu.
Increment Sistem Bilangan
Seperti uraian di atas bahwa increment berarti bilangan sebelumnya akan ditambah dengan 1.

Decrement Sistem Bilangan
Decrement didapatkan dengan cara mengurangi bilangan sebelumnya dengan 1.
Sebagai contoh:

Comments
Post a Comment